wher 101;&#EModulus tânăr,-Imomentul inerției diametrale a secțiunii arborelui;-k initmh unitate 8211; coeficientul de rigiditate a momentului al unei legături echivalente care corespunde crăpăturii deschise pe deplin. Ecuația are două summituri /821; flexibilitate legată de fisura și flexibilitatea fasciculului fără fisură.Acesta

 trebuie remarcat faptul că, indiferent de forma fasciculului, condițiile limită și poziția fisurii, poziția sa contribuția la flexibilitatea general ă a fasciculului depinde numai de coeficient k initmh ,Adică primul summit. În timp ce fascicul se roteşte, flexibilitatea în secţiunea fisură se schimbă.Noi obținem următoarele:wher 101; 

 g O&#flexibilitate a fasciculului fără fisură;  q)=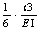 -kmhcoeficientul actual de rigiditate a momentului pentru dataqBine. -Integrarea a două ecuații (5) și (7), obținem:wher101;luând în considerare ecuația (6) obținem legea schimbării rigidității momentului în funcție de diferența de fază

 es q 

 :Rezistența de moment obținută a unei legături echivalente depinde numai de diametrul arborelui, caracteristicile materialului și adâncimea fisurii.Schimbarea poziției fisurii în arbore, caracteristicile arborelui, inclusiv unitățile de suport, nu modifică rigiditatea de moment a unei legături echivalente (pe&#cu condiţia ca secţiunea cu fisură să rămână aceeaşi în orice parte a secţiunii cu fisură pentru care a fostobținut).Mergând înapoi la matricea de rigiditate obținute înainte, coeficienții de rigiditate sale pot fi scrise ca următoarele: wher 

101; k

init 

 ee , k  init 

 UH valorile inițiale ale rigidității momentului la axele corespunzătoare pentru crăpătura complet deschisă&#Bine. Sarcina de kinit ee,kinit  -UHcalculul poate fi rezolvat în două moduri.Primul este calcularea rigidității momentului în programul FEM.Al doilea este să folosim teoria mecanicii fracturilor.Aceasta oferă posibilitatea de a calcula valorile coeficienților de flexibilitate local ă a fisurii deschise în cazul în care geometria, diametrul arborelui și caracteristicile materialului sunt cunoscute [7,10].

 Algoritm pentru a simula sistemul rotor cu fisură Următorii pași ar trebui trecuți pentru a obține coeficienți de rigiditate de moment a fisurii.1. Modelul complet de rotor este creat într-unul dintre programele specializate pentru a analiza dinamica rotorului (pentrude exemplu, în Dynamics R4).2. Secţiunea rotorului cu crăpătură este subliniată.  O fisură împarte secţiunea de puţuri în două subsisteme.Legătura descrisă de matricea variabilelorcoeficienți de rigiditate[K (q 

 , 

j)

de

dimensiunea 6x6 este plasată între subsisteme.

4. Coeficienți inițiali ai rigidității momentului

k

init

ee ,kinitUHpentru crack deschis sunt obținute prin metodele dateSus.Aceste date sunt iniţiale pentru calcul.Coeficienții matricei rigide ale legăturii simulând fisura sunt calculați în timp ce integrarea ecuațiilor de mișcare 

a sistemului rotor pentru fiecareqBine.La ecuația matricei neliniare care descrie modelul dinamic neliniaral sistemului rotor este următorul: wher101;[M ]

unitate 8211; matrice de coeficienți inerțiali;

 [ C ]

unitate 8211; matrice de coeficienți de amortizare și giroscopuri;[K

] 

 Matricea de coeficienți de rigiditate; {Y:bi}&#u},{Y:bi}u},{Y:bi}u}unitate 8211; coloane de accelerații vibraționale, viteze de vibrație și deplasări vibraționale corespunzătoare;{Y:bi}-F(t)}&&orice tipuri de sarcini dinamice – 82211; interne și externe.Matricea de rigiditate a unei legături echivalente poate fi împărțită în două părți: constant ă și variabilă, iar următoarele sunt adevărate:[&K CEste inclusă în matricea general ă de rigiditate a[K]Sistem.Matrice() [q j] n,Keste utilizat pentru a calculareacții ale unei legături neliniare:-wher101; 

 u RX , 

 u rCommentTual rotații ale secțiunilor în jurul axelor corespunzătoare.Ecuația de mișcare final ă a sistemului este următoarea:Ecuația dată poate fi rezolvată prin metode numerice, cum ar fi RungeMetoda Kutta, metoda Newmark, etc.Adecvarea algoritmului sugerat se face prin compararea flexibilității celor douăfascicul de sprijin cucrack obținut în finitelement sistem și în conformitate cu presupusul algoritm în Dynamics R4.Sarcina este de a calcula deformarea fasciculului sub for ță unitară în secțiunile fisură pentru diferite faze între fisură și forță.Figura 3 arată rezultatele verificării algoritmului sugerat.Se compară trei rezultate:flexibilitatea se calculează utilizând metoda elementului finit (FEM).În FEM se calculează flexibilitatea radială a modelului fasciculului cu crăpătură

sistem pentru întreaga gamă de poziții unghiulare ale fisurii;&#flexibilitatea se calculează utilizând Dynamics R4, datele inițiale sunt obținute cu ajutorul FEM.Valorile inițiale ale momentuluirigiditate pentru crack complet deschisk initee, kinit

UHsunt obținute ecuația de rezolvare (7) pentru

k-init

mh-și flexibilitatea radial ă a fasciculului cu crăpătură

gc-la direcția corespunzătoare se calculează utilizând FEM.Rezistența momentului pentru pozițiile intermediare de fisură unghiulară se schimbă de la minimum la maxim în conformitate cu legea (10);

flexibilitatea se calculează utilizând Dynamics R4.Date inițiale privind flexibilitatea momentului pentru crack complet deschis

-k-ee

 init , k-UH  

initsunt obținute analitic utilizând algoritmii mecanicii de fractură [7, 10].Valoarea flexibilității momentului pentrupozițiile unghiulare intermediare de fisură se schimbă de la minimum la maxim în conformitate cu legea (10).Figura 3 Modificarea flexibilității fasciculului în sectorul fisurilor per revoluție Rezultatele în calculul FEMModelele şi modelele din Dynamics R4 sunt apropiate.Rezultatele de calcul cu condiții inițiale obținute în mod analitic diferă de rezultatele FEM mai mici de 1%.În același timp, rigiditatea inițială este calculată analitic mult mai rapid decât calculul FEM și necesită mai puțin ore de muncă și atât de ușorlaUtilizare.  Geometrie și parametri ai rotorului cu fisură Geometria rotorului cu crăpătură este aleasă pentru a arăta algoritmul de lucru în cel mai bun avantaj, Tabelul 1.rotorul cu discul central, suporturile sunt plasate la capetele arborelui.② ②②②

 ② ②-②②②②②②②②②  ② 

②

 ② ② ②-②-②-② 

②

 ② ② ②